dice game (text mode)

This tutorial shows you how to create a computer game based on the rules of the pen and paper game →Yahtzee, a game about dice throwing. This tutorial will only use Python and no other third party libraries.

The user interface of the computer game that you will build in this tutorial will be a text based user interface. Later tutorials will improve the game by adding a graphical user interface.

lesson goal

• problem solving: adapting a physical dice game to a computer game using Python.

• writing functions to code the game rules in Python

  • testing those functions

• writing a playable computer game in Python

preparation

• warming up:

  • read the rules of “Yahtzee” or similar games:

  • Yahtzee: https://en.wikipedia.org/wiki/Yahtzee

  • Yacht: https://en.wikipedia.org/wiki/Yacht_(dice_game)

  • Poker Dice: https://en.wikipedia.org/wiki/Poker_Dice

  • Generala: https://en.wikipedia.org/wiki/Generala

  • See http://www.yahtzee-rules.com/ for alternative Yahtzee rules

  • prepare five dice. Each die has six sides, representing numbers from 1 to 6.

  • print out a score table: pdf odg

  • play some rounds of “Yahtzee” without computer

• Software:

  • make sure Python is installed on your computer: see https://python.org

game rules

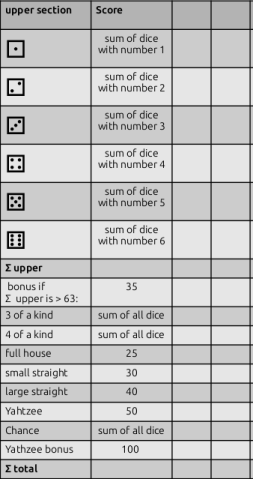
Figure 1: score table (part)

The pen_and_paper version of Yahtzee and similar dice games is played with 5 dice, a pen and a (paper) score table. The score table (see Figure 1 at right) has 13 lines, each linerepresenting an option that the player can play. Those options are named similar to the figures of the card game →poker and have names like “full house”, “three of a kind” or “Yathzee”.

The game rules are:

• Each player had 5 dice and can throw them 3 times per game round.

• The game has 13 game rounds.

• After the first and the second throw the player can decide to throw some, all or none of his dice again or leave them.

• After the third throw, the player must play one of the 13 possible options. When the dice match with the chosen options, the player gets points for this round. Otherwise they get zero points. In both cases, the selected option is “used up” for the rest of the game.

• The options consist of an upper section (1,2,3,4,5,6) and a lower section (“three of a kind”, “four of a kind”, “full house”, “small straight”, “large straight”, “yahtzee”, “chance”). The scores of each options are:

upper section

Aces:

the sum of dice with the number one

Twos:

the sum of dice with the number two

Threes:

the sum of dice with the number three

Fours:

the sum of dice with the number four

Fives:

the sum of dice with the number five

Sixes:

the sum of dice with the number six

Example: the player throws 2 sixes and 3 other numbers. He decide to play the Sixes option. His score is 2 x 6 = 12 points.

lower section

three of a kind:

Sum of all dice. 0 points if less than 3 dice show the same number.

four of a kind:

Sum of all dice. 0 points if less than 4 dice show the same number.

full house:

25 points. 0 points if there are no 3 dice with the same number and 2 dice with (another) same number.

small straight:

30 points if 4 dice show the combination 1,2,3,4 or 2,3,4,5 or 3,4,5,6. Otherwise 0 points.

large straight:

40 points if 5 dice show the combination 1,2,3,4,5 or 2,3,4,5,6. Otherwise 0 points.

Yahtzee:

50 points if 5 dice show the same number, otherwise 0 points.

Chance:

sum of all dice

special rules

Yathzee bonus:

If the player throws a Yahtzee and has already filled the Yahtzee box with a score of 50, they score a Yahtzee bonus and get an extra 100 points. However, if they throw a Yahtzee and have used the Yahtzee category already with a score of 0, they do not get a Yahtzee bonus.

Joker:

A yahtzee can act as full house, small street or large street if the upper section with the dice number has already been used and the Yahtzee option in the lower section has also been used.

upper section bonus:

If the player scores more than 63 points in the upper section, they get a bonus of 35 points.

divide task into small tasks

The big task of this tutorial is to write a Yahtzee computer game. There is no single perfect way of how to do this. In fact, every programmer may come up with one (or many!) slightly different versions.

A sensible approach is to split a big task into smaller, more managable sub-tasks. It is helpful to write down what the program should do:

• Simulate throwing of five dice

• Let the player keep some dice / throw some dice

• Keep track of game round and throws (3 throws per game round, 13 game rounds)

• Once per game round: Show the player which options they can play and how many points they will get for each option. This includes:

  • Recognizing if the player throwed a specific option (full house, large straight etc.)

  • Calculating the amount of points the player would get for each option. This includes:

    • Apply special rules such a joker rule (yahtzee can act as a joker under certain conditions)

• Ask the player to choose an option and keep track of already played (used) options

• Keep track of points, calculate sum of points at the end of the game. This includes:

  • Calculating upper score bonus and yahtzee bonus

If the program works, it needs testing:

• to make sure that the user can not “break” the game by entering silly or wrong commands

• to make sure that the scoring is correct according to the game rules

Let’s solve all of those sub-tasks listed above step by step:

---

step one

task:

simulate throwing of five dice

To simulate the throwing of five dice, it is necessary to import Python’s bulit-in random module and call the random.randint() function. The result of each function call need to be stored in a variable. Here five different variables (d1…d5) are used:

dicgame01_01.py

source code

import random             # ❶	
d1 = random.randint(1,6)  # ➋
d2 = random.randint(1,6)
d3 = random.randint(1,6)  	
d4 = random.randint(1,6)
d5 = random.randint(1,6)
print(d1,d2,d3,d4,d5)     # ➌

output

example output of dicegame01_01.txt (Your output may be different)

5 6 5 1 5

code explained

➀:

It is necessary to import the random module first before being able to call the the random.randint() function

➁:

assigning of a value to a variable: the variable (d1..d5) is written left of the = sign, the value is written right of it. The value itself is in this case the result (the return value) of a function call to the random.randint() function.

➂:

print() out all variables in one single row. The comma (,) between the variables creates an space. This line could also be written using an f-string:

print(f"{d1} {d2} {d3} {d4} {d5}")

Having five different variables for for the five simulated dice is fine, but having a single data structure to store all of those 5 numbers together is more practical.

The datastructure should be iterable (to process all five dice one-by-one) and it should be mutable to allow the replacing of specific numbers. Python’s most popular datastructure, the list fullfills both criteria. The code example below creates such a list holding five random values:

dicgame01_02.py

source code

import random
dicelist = []                            # ➊
for _ in range(5):                       # ➋
    dicelist.append(random.randint(1,6)) # ➌  
print(dicelist)                          # ➍

output

example output of dicegame01_02.txt (Your output may be different)

[6, 2, 2, 1, 5]

diff

diff between dicegame01_01.py -> dicegame01_02.py

--- /home/horst/code/sphinx_playground/source/dicegame/dicegame01_01.py
+++ /home/horst/code/sphinx_playground/source/dicegame/dicegame01_02.py
@@ -1,7 +1,5 @@
-import random             # ❶	
-d1 = random.randint(1,6)  # ➋
-d2 = random.randint(1,6)
-d3 = random.randint(1,6)  	
-d4 = random.randint(1,6)
-d5 = random.randint(1,6)
-print(d1,d2,d3,d4,d5)     # ➌+import random
+dicelist = []                            # ➊
+for _ in range(5):                       # ➋
+    dicelist.append(random.randint(1,6)) # ➌  
+print(dicelist)                          # ➍

code explained

➀:

creating an empty list and assigning it to the variable dicelist

➁:

using a for loop and the range() function to repeat (the next line of) code 5 times. Note that this for loop has no typical loop variable (like x, y, i etc.) but uses instead an underscore: _. This is to indicate that the loop variable will not be used in any calculations.

➂:

This code line will be repeated 5 times: Generating a random number between 1 and 6 and using list.append() to add it at the end of the existing ‘dicelist’.

➃:

print out all elements of ‘dicelist’.

One sub-task done, four more to go:

• simulate throwing 5 dice

• let the player keep some dice / throw some dice

• keep track of game round and throws

• ask the player to choose an option and keep track of played options

• show the player how many points they will get for each option

• calculate sum of points at the end of the game

step two

task:

let the player keep some dice / throw some dice

task:

keep track of game round and throws

The progrm should provide a way for the user to tell the program which of the five dice they want to keep and which dice they want to throw again. In short, a user interface is needed.

This leads to a new problem: How can the user tell the computer which of the five dice they want to keep ?

Several solutions are possible:

• Asking the user which elements of dicelist they want to keep. Example: The user throws two sixes and three other numbers. The user types the number 6 to indicate that they want to keep all sixes.

  Problem: What if they want to keep only one six? A second follow-up question would be necessary to ask how many sixes they want to keep. And of course, testing is necessary to make sure the user only enters numbers that exist in dicelist in the desired quantity.

• Giving each die an index and asking the user to type in the indexes of the dice they want to keep. Python automatically gives an index to each item of a list (starting with zero!). Example output:

  index       0  1  2  3  4
  dicelist: [ 5, 6, 6, 3, 1]    
  

  Problem: Both the index and results of the dice throws are numbers (0-4 and 1-6), making the user experience a bit confusing. The fact that Python starts indexing with 0 and not with 1 makes the whole process a bit counter-intuitive.

• Giving each die a letter (a,b,c,d,e) and asking the user to type the letter(s) of the dice they want to keep. The index of the desired dicelist item is then calculated from the entered letter. Example output:

  letters:    a  b  c  d  e
  dicelist:  [5, 6, 6, 3, 1] 
  

This tutorial will continue with the third variant (giving each position in dicelist a letter).

A simple prototype for the user interface could look like this:

dicgame01_03.py

source code

import random
dicelist = [5,1,4,4,2]                # ➊
print("old dicelist:")
print(" a  b  c  d  e")               # ➋
print(dicelist)
text = "Type letter(s) of dice you want to keep and press ENTER "
command = input(text)                 # ➌        
if not "a" in command:                # ➍
    dicelist[0] = random.randint(1,6) # ➎
if not "b" in command:
    dicelist[1] = random.randint(1,6)
if not "c" in command:
    dicelist[2] = random.randint(1,6)
if not "d" in command:
    dicelist[3] = random.randint(1,6)
if not "e" in command:
    dicelist[4] = random.randint(1,6)
print("new dicelist:", dicelist)

output

output of dicegame01_03.py

old dicelist:
 a  b  c  d  e
[5, 1, 4, 4, 2]
Type letter(s) of dice you want to keep and press ENTER cd
new dicelist: [4, 5, 4, 4, 6]

diff

diff between dicegame01_02.py -> dicegame01_03.py

--- /home/horst/code/sphinx_playground/source/dicegame/dicegame01_02.py
+++ /home/horst/code/sphinx_playground/source/dicegame/dicegame01_03.py
@@ -1,5 +1,18 @@
 import random
-dicelist = []                            # ➊
-for _ in range(5):                       # ➋
-    dicelist.append(random.randint(1,6)) # ➌  
-print(dicelist)                          # ➍+dicelist = [5,1,4,4,2]                # ➊
+print("old dicelist:")
+print(" a  b  c  d  e")               # ➋
+print(dicelist)
+text = "Type letter(s) of dice you want to keep and press ENTER "
+command = input(text)                 # ➌        
+if not "a" in command:                # ➍
+    dicelist[0] = random.randint(1,6) # ➎
+if not "b" in command:
+    dicelist[1] = random.randint(1,6)
+if not "c" in command:
+    dicelist[2] = random.randint(1,6)
+if not "d" in command:
+    dicelist[3] = random.randint(1,6)
+if not "e" in command:
+    dicelist[4] = random.randint(1,6)
+print("new dicelist:", dicelist)

code explained

➀:

This examples is only about the user interface and not about the random number generation. It assumes that a dicelist with five random numbers exist already.

➁:

printing letters instead of the indexes. Note the leading space before a. The letters will appear exaclty over the elements of dicelist. (See output).using a for loop and the range() function to repeat (the next line of) code 5 times. Note that this for loop has no typical loop variable (like x, y, i etc.) but uses instead an underscore: _. This is to indicate that the loop variable will not be used in any calculations.

➂:

The input() command displays the prompt (in this case, the variable text) and waits that the user types something on the keyboard. Whatever the user types will be stored in the variable command.

➃:

testing if the string "a" is not inside the string command. Note that Python is case sensitive, this program only checks for an a but not for an A!

➄:

replace the first element of dicelist with a new random number (see random.randint()). Python starts indexing with 0, therefore the dicelist[0] referrs to the first element, dicelist[1] referrs to the second element etc. See list.

The beauty of this user interface is that it does not matter if the user enter letters (or numbers, punctuation etc) or if they enter the same letter several times … it still works.

By merging dicegame01_02.py together with dicegame01_03.py, putting everything inside of a nested loop (13 game rounds, 3 throws per game) and making the user interface a bit more idiot-proof so that it does not matter if the user type letters in lowercase or UPPERCASE we have an already playable version of the dicegame. As an undemanded extra feature, version dicegame01_04.py below shows at the end of the game an “history” (a list of dicelists) of every game round (It shows what the value of dicelist was).

dicgame01_04.py

source code

import random

history = []                                      
   
for game_round in range(1,14):                    # ➊ 
    dicelist = []                                     
    for _ in range(5):    
        dicelist.append(random.randint(1,6))  
    print(f"-------- round {game_round} of 13--------------")  # ➋
    for throw in (1,2,3):                         # ➌
        text= "throw: {} of 3".format(throw)      # ➍
        print(text)
        print(" a  b  c  d  e")
        print(dicelist)
        if throw < 3:
            text = "Type letter(s) of dice to keep and press ENTER "
            command = input(text).lower()              # ➎
            for i, char in enumerate("abcde") :        # ➏ 
                if char not in command:                
                    dicelist[i] = random.randint(1,6)  # ➐ 

        
    print(f"------- end of round {game_round}------")
    if game_round == 13:                       # ➑
        text = "press ENTER to see the history of dice throws"
    else:
        text = "press ENTER to start the next game round"
    input(text)                           # ➒  
    history.append(dicelist.copy())       # ➓
print("Game Over")  
print("--- history of your dice throws: ---")
print("game round,  result")
for game_round, result in enumerate(history, 1):  # ⓫ 
    print(f"{game_round:>5} : {result}" )         # ⓬

output

example output of dicegame01_04.py (Your output may be different)

-------- round 1 of 13--------------
throw: 1 of 3
 a  b  c  d  e
[1, 6, 6, 2, 2]
Type letter(s) of dice to keep and press ENTER bc
throw: 2 of 3
 a  b  c  d  e
[3, 6, 6, 3, 6]
Type letter(s) of dice to keep and press ENTER bce
throw: 3 of 3
 a  b  c  d  e
[4, 6, 6, 2, 6]
------- end of round 1------
press ENTER to start the next game round
-------- round 2 of 13--------------
throw: 1 of 3
 a  b  c  d  e
[3, 3, 5, 4, 3]
Type letter(s) of dice to keep and press ENTER abe
throw: 2 of 3
 a  b  c  d  e
[3, 3, 6, 3, 3]
Type letter(s) of dice to keep and press ENTER abde
throw: 3 of 3
 a  b  c  d  e
[3, 3, 3, 3, 3]
------- end of round 2------
press ENTER to start the next game round
-------- round 3 of 13--------------

(snipp)

-------- round 13 of 13--------------
throw: 1 of 3
 a  b  c  d  e
[6, 6, 5, 2, 2]
Type letter(s) of dice to keep and press ENTER ab
throw: 2 of 3
 a  b  c  d  e
[6, 6, 3, 3, 3]
Type letter(s) of dice to keep and press ENTER abcde
throw: 3 of 3
 a  b  c  d  e
[6, 6, 3, 3, 3]
------- end of round 13------
press ENTER to see the history of dice throws
Game Over
--- history of your dice throws: ---
game round,  result
    1 : [4, 6, 6, 2, 6]
    2 : [3, 3, 3, 3, 3]
    3 : [2, 1, 2, 1, 2]
    4 : [1, 1, 2, 5, 1]
    5 : [3, 5, 3, 1, 2]
    6 : [3, 6, 3, 4, 1]
    7 : [6, 2, 6, 1, 5]
    8 : [4, 3, 2, 3, 6]
    9 : [6, 1, 5, 5, 4]
   10 : [4, 3, 2, 3, 1]
   11 : [4, 4, 4, 6, 1]
   12 : [2, 6, 3, 4, 5]
   13 : [6, 6, 3, 3, 3]

diff

diff between dicegame01_03.py -> dicegame01_04.py

--- /home/horst/code/sphinx_playground/source/dicegame/dicegame01_03.py
+++ /home/horst/code/sphinx_playground/source/dicegame/dicegame01_04.py
@@ -1,18 +1,34 @@
 import random
-dicelist = [5,1,4,4,2]                # ➊
-print("old dicelist:")
-print(" a  b  c  d  e")               # ➋
-print(dicelist)
-text = "Type letter(s) of dice you want to keep and press ENTER "
-command = input(text)                 # ➌        
-if not "a" in command:                # ➍
-    dicelist[0] = random.randint(1,6) # ➎
-if not "b" in command:
-    dicelist[1] = random.randint(1,6)
-if not "c" in command:
-    dicelist[2] = random.randint(1,6)
-if not "d" in command:
-    dicelist[3] = random.randint(1,6)
-if not "e" in command:
-    dicelist[4] = random.randint(1,6)
-print("new dicelist:", dicelist)
+
+history = []                                      
+   
+for game_round in range(1,14):                    # ➊ 
+    dicelist = []                                     
+    for _ in range(5):    
+        dicelist.append(random.randint(1,6))  
+    print(f"-------- round {game_round} of 13--------------")  # ➋
+    for throw in (1,2,3):                         # ➌
+        text= "throw: {} of 3".format(throw)      # ➍
+        print(text)
+        print(" a  b  c  d  e")
+        print(dicelist)
+        if throw < 3:
+            text = "Type letter(s) of dice to keep and press ENTER "
+            command = input(text).lower()              # ➎
+            for i, char in enumerate("abcde") :        # ➏ 
+                if char not in command:                
+                    dicelist[i] = random.randint(1,6)  # ➐ 
+
+        
+    print(f"------- end of round {game_round}------")
+    if game_round == 13:                       # ➑
+        text = "press ENTER to see the history of dice throws"
+    else:
+        text = "press ENTER to start the next game round"
+    input(text)                           # ➒  
+    history.append(dicelist.copy())       # ➓
+print("Game Over")  
+print("--- history of your dice throws: ---")
+print("game round,  result")
+for game_round, result in enumerate(history, 1):  # ⓫ 
+    print(f"{game_round:>5} : {result}" )         # ⓬

code explained

➀:

See for loops and the range() function: The indented code block below (lines 6 - 29) will be repeated 13 times.

➁:

See f-string. The string inside the print() function has an f prefix. In the output, the value of the variable game_round will be placed inside the string instead of the {game_round} placeholder.

➂:

It is not always necessary to use range() together with for loops… any iterable will do. In this case, the tuple (1,2,3). The line could also be written as:

    for throw in range(1,4):

In both cases, the indented code block below (lines 11-20) is repeated 3 times.

➃:

See string.format(): Using the string method .format() is very similar to using f-strings. The {} placeholder will be replaced in the output with the value of the variable throw.

➄:

more idiot-proof than dicelist01_03.py: The string.lower() method converts the result of the input() function into lowercase and only this (lowercase) result will be stored in the variable command.

➅:

Take a look at dicegame01_03.py: Instead of using five different if commands the enumerate() function is used: Each letter of the string abcde gets an index (starting with 0). The index is saved assigned to the variable i, the letter is assigned to the variable char.

➆:

If the user did not typed the corresponding letter to keep this element of dicelist, it will be replaced with a new random number. Note that this happens only after the first and after the second throw (See if command in line 15 and else command in line 22).

➇:

See ==: Two equal signs next to each other in Python are a comperation (testing if the left part is equal to the right part).

➈:

This input() function waits that the user press the ENTER key. Whatever the user types in is (before hitting ENTER) is simply ignored.

➉:

A whole copy of the current dicelist (a list) is appended to history (also a list). See list.copy(). The same line could also be written as:

        history.append(dicelist[:]) 

In the end, history is a list of lists or a nested list.

⑪:

using enumerate() again (see ➅), but this time the index (assigned to the variable game_round) must start with 1 instead of 0.

⑫:

See Format Specification Mini Language. the :>5 suffix inside the {game_round} placeholder right-aligns the value of the variable game_round and set it’s width to 5 chars.

Attention

at line 29 (#⑪), What would happen if you do not append a copy of dicelist to history but instead just dicelist:

        history.append(dicelist)   #  ⑪

Modify the code as shown above, play a full game of 13 game rounds and look at the output of history to find out!

Score calculation and the choosing of an option per game round is still lacking but three sub tasks already are done:

• simulate throwing 5 dice

• let the player keep some dice / throw some dice

• keep track of game round and throws

• ask the player to choose an option - - [ ] show the player how many points they will get for each option

• calculate sum of points at the end of the game

step three

task:

ask the player to choose an option and keep track of played options

A data structure is needed to hold the options a player can choose at each game round. One possibility is to use a list:

all_options = [    
    # upper section:
    "Ones","Twos", "Threes", "Fours", "Fives","Sixes", 
    # lower section:
    "Three Of A Kind", "Four Of A Kind", "Full House",
    "Small Straight", "Large Straight", "Yahtzee", "Chance",
    ]

For the task of keeping track of played options:

As always there are several possibilities of how to design code and data structures.

Below are just some possible solutions sketched for the problem of keeping track of played and unplayed options:

using lists

Create a copy of a list and use the .append() and .remove() methods of list:

all_options = [    
    "Ones","Twos", "Threes",  # etc.
    "Full House", "Chance",  # etc.
]
unplayed = all_options.copy()
played = [] # empty list
player_choice = "Full House"
played.append(player_choice)
unplayed.remove(player_choice)
print(unplayed)

list and set

create a set out of a list and use the .difference() methods of sets:

all_options = [    
    "Ones","Twos", "Threes",  # etc.
    "Full House", "Chance",  # etc.
]
played = []
player_choice = "Full House"
played.append(player_choice)
unplayed = set(all_options).difference(
    set(played))
print(unplayed)

dictionary and list comprehension

create a dictionary with the option names as keys and a boolean value as values to indicate if the option was played. Update the dictionary when an option is played and calculate the unplayed options by using a list comprehension:

all_options = [    
    "Ones","Twos", "Threes",  # etc.
    "Full House", "Chance",  # etc.
]
played = {"Ones": False, 
          "Twos": False,
          "Threes": False,
          "Full House": False,
          "Chance":False,
          # etc.
          }
player_choice = "Full House"
played[player_choice] = True # update the dictionary
unplayed = [o for o in all_options
    if not played[o]]
print(unplayed)

Syncronize lists with common index

Have two lists with the same lenght: all_options and played. The latter consist of boolean values. Use the .index() methods of lists to find out the index of the played option and update the played. Use a list comprehension to calculate the unplayed options:

all_options = [    
    "Ones","Twos", "Threes",  # etc.
    "Full House", "Chance",  # etc.
]
played = [False for o in all_options]
# [False, False, False, ...]  # etc. 
player_choice = "Full House"
# find out the index of this option
i = all_options.index(player_choice)
# i has value of 3 in this example
# update played:
played[i] = True
# list comprehension
unplayed = [o for o in all_options
    if not played[all_options.index(o)]
    ]
print(unplayed)

TODO: data class

Thinking a bit ahead, a good question to ask is: what information is connected with the list of options?

• the name of the option

• the maximum possible score for this option

• if this option is still playable (or was already played)

• the archived score for this option - if the option was played at all. (Attention: An option can be played with an score of 0, so a score of 0 does not mean the option was not yet played)

The maximum possible score is fixed for each option and will not change during a game. Therefore, a immutable datastructure like a tuple makes sense:

# list of tuples: (option name, max_score)
all_options = [("Ones", 5),
               ("Twos",10),
               ("Threes", 15),
               # etc.
               ]

But a dictionary is also possible (and a bit more beautiful to look at):

# key: name of option.     
# value: maximum possible score for this option
#           keys:            values:
options = {  
                                       # upper section:
           "Ones":            5,
           "Twos":            10,
           "Threes":          15,
           "Fours":           20,
           "Fives":           25,
           "Sixes":           30,
                                        # lower section
           "Three Of A Kind": 30,
           "Four Of A Kind":  30,
           "Full House":      25,
           "Small Straight":  30,
           "Large Straight":  40,
           "Yahtzee":         50,
           "Chance":          30,
           }

menu for options

The user need some way to indicate to the Python program the kind of option they want to play. In contrast to the letter-menu of dicegame01_04.py, (where the player can choose to keep some of the five dice) the player must choose an option to play. Just hitting the Enter key or typing in an invalid choice is (to indicate “keep no dice”) is not valid when choosing one of the 13 possible options to play.

The menu for choosing an option to play must therefore run inside of a endless loop until the user makes a valid choice.

As always, several possibilities to code such an menu exist.

type name

The most straight-forward way would be to let the user type in exactly the name of the desired option:

dicgame01_04a.py

source code

# example code: menu where user must type exact name
#        option name        max. score
all_options = {  
                                       # upper section:
           "Ones":            5,
           "Twos":            10,
           "Threes":          15,
           "Fours":           20,
           "Fives":           25,
           "Sixes":           30,
                                        # lower section
           "Three Of A Kind": 30,
           "Four Of A Kind":  30,
           "Full House":      25,
           "Small Straight":  30,
           "Large Straight":  40,
           "Yahtzee":         50,
           "Chance":          30,
           }
# display the menu
print("please choose one option of those:")
print("name             max. points")
for name, maximum_points in all_options.items(): # ➊
    print(f"{name:<15}  {maximum_points:>2}")    # ➋
# validate input
while True:                                      # ➌ 
    command = input("Write the name of option: >>>")
    if command in all_options:
        option = command
        break                                    # ➍
    print("strange input. Please try again.")
# user made a valid choice
print("you choose to play", option )             # ➎

output

output of dicegame01_04a.txt

please choose one option of those:
name             max. points
Ones              5
Twos             10
Threes           15
Fours            20
Fives            25
Sixes            30
Three Of A Kind  30
Four Of A Kind   30
Full House       25
Small Straight   30
Large Straight   40
Yahtzee          50
Chance           30
Write the name of option: >>>full house
strange input. Please try again.
Write the name of option: >>>Full House
you choose to play Full House

code explained

➀:

all_options.items() generates from the dictionary all_options a list of tuples with (key, value) pairs: [("Ones", 5), ("Twos", 10), ...etc.]. The for loop iterates over this list and assigns values to the variables name (the name of the option) and maximum_points.

➁:

printing a beautiful menu using f-string. The numbers behind the colon inside of the curly brackets align the strings and give them a minimum width. See Format Specification Mini Language.

➂:

Start of an endless loop because nobody can predict how many attempts the user needs before they will make a valid choice. The indented code block below (lines 27-31) will be repeated as often as necessary.

➃:

The break statement escapes out of the loop, the program flow continues at line 32

➄:

This line will only be executed if the user sucessfully made a valid choice in the menu (and by doing so escaped the endless loop)

The code is clean and elegant code, but lacks in the category “user friendly”: Typing in the option names, including correct lower case / upper case characters, is slow. And not much fun.

single letter

Another variant is to use the same approach as in dicegame01_04.py.. use a letter for each option. The Yahtzee game has a maximum of 13 options, the alphabet has more than enough letters.

dicgame01_04b.py

source code

# dictionary of option name and maximum score
all_options = {  
                                       # upper section:
           "Ones":            5,
           "Twos":            10,
           "Threes":          15,
           "Fours":           20,
           "Fives":           25,
           "Sixes":           30,
                                        # lower section
           "Three Of A Kind": 30,
           "Four Of A Kind":  30,
           "Full House":      25,
           "Small Straight":  30,
           "Large Straight":  40,
           "Yahtzee":         50,
           "Chance":          30,
           }

# string with l3 letters for menu options
abc = "abcdefghijklm"

# write menu and display maximum points for each option
print("please choose one option of those:")
print("letter  name         max. score")
for letter, (name, max_score) in zip(abc,all_options.items()): # ➊
    print(f"{letter:>5}: {name:<15}  {max_score:>2}")          # ➋
# endless loop until a valid option is choosen
while True:                                                    # ➌
    command = input("Type the letter for an option: >>>")
    if len(command) == 1 and command in abc:                   # ➍
        option = list(all_options.keys())[abc.index(command)]  # ➎
        break
    print("strange input. Please try again.")
print("you choose to play", option )

output

output of dicegame01_04b.txt

please choose one option of those:
letter  name         max. points
    a: Ones              5
    b: Twos             10
    c: Threes           15
    d: Fours            20
    e: Fives            25
    f: Sixes            30
    g: Three Of A Kind  30
    h: Four Of A Kind   30
    i: Full House       25
    j: Small Straight   30
    k: Large Straight   40
    l: Yahtzee          50
    m: Chance           30
Type the letter for an option: >>>x
strange input. Please try again.
Type the letter for an option: >>>J
strange input. Please try again.
Type the letter for an option: >>>j
you choose to play Small Straight

diff

diff between dicegame01_04a.py -> dicegame01_04b.py

--- /home/horst/code/sphinx_playground/source/dicegame/dicegame01_04a.py
+++ /home/horst/code/sphinx_playground/source/dicegame/dicegame01_04b.py
@@ -1,5 +1,4 @@
-# example code: menu where user must type exact name
-#        option name        max. score
+# dictionary of option name and maximum score
 all_options = {  
                                        # upper section:
            "Ones":            5,
@@ -17,17 +16,20 @@
            "Yahtzee":         50,
            "Chance":          30,
            }
-# display the menu
+
+# string with l3 letters for menu options
+abc = "abcdefghijklm"
+
+# write menu and display maximum points for each option
 print("please choose one option of those:")
-print("name             max. points")
-for name, maximum_points in all_options.items(): # ➊
-    print(f"{name:<15}  {maximum_points:>2}")    # ➋
-# validate input
-while True:                                      # ➌ 
-    command = input("Write the name of option: >>>")
-    if command in all_options:
-        option = command
-        break                                    # ➍
+print("letter  name         max. score")
+for letter, (name, max_score) in zip(abc,all_options.items()): # ➊
+    print(f"{letter:>5}: {name:<15}  {max_score:>2}")          # ➋
+# endless loop until a valid option is choosen
+while True:                                                    # ➌
+    command = input("Type the letter for an option: >>>")
+    if len(command) == 1 and command in abc:                   # ➍
+        option = list(all_options.keys())[abc.index(command)]  # ➎
+        break
     print("strange input. Please try again.")
-# user made a valid choice
-print("you choose to play", option )             # ➎+print("you choose to play", option )

code explained

➀:

A lot happens in this line, let’s break it down:

1. all_options.items() generates from the dictionary all_options a list of tuples with (key, value) pairs: [("Ones", 5), ("Twos", 10), ...etc.].

2. zip() combines two iterables so that a for loop can iterate over both of them at the same time. In this case, the first letter of the abc string (a) is matched with the first tuple from all_options.items() list: ("Ones", 5).

3. One single for loop iterates over the zip-list and assigns values to the variables letter (the character of the abc string) name (the name of the option) and max_score (the maximum possible score for this option).

➁:

printing a beautiful menu using f-string. The numbers behind the colon inside of the curly brackets align the strings and give them a minimum width. See Format Specification Mini Language.

➂:

Create an endless loop because nobody can predict how many attempts the user needs before they will make a valid choice. The indented code block below (lines 30-334) will be repeated as often as necessary.

➃:

Testing if the user made a valid choice: If the length of the variable command is 1 and command is also a part of the abc string then…

➄:

break out of the endless loop. But before breaking, assing to the variable option the name of the selected option. To do so, the choosen menu letter (assigned to the variable command) is used to calculate the corresponding option name:

1. Create a list out of the keys from the dictionary all_options.

2. Calculate the index (starting with 0!) of the choosen menu letter inside the abc string.

3. Use this index to get the matching option name by element with this index out of the list created at step 1.

numbers

Another variant (used in this tutorial) is to give each playable option an unique number and let the user type in those numbers in the menu:

dicgame01_04c.py

source code

# dictionary: key: option name, value:  maximum score
all_options = {  
                                       # upper section:
           "Ones":            5,
           "Twos":            10,
           "Threes":          15,
           "Fours":           20,
           "Fives":           25,
           "Sixes":           30,
                                        # lower section
           "Three Of A Kind": 30,
           "Four Of A Kind":  30,
           "Full House":      25,
           "Small Straight":  30,
           "Large Straight":  40,
           "Yahtzee":         50,
           "Chance":          30,
           }

# write menu and display maximum points for each option
print("please choose one option of those:")
print("letter  name         max. score")
for number, (name, max_score) in enumerate(all_options.items(), 1): # ➊
    print(f"{number:>2}: {name:<15}  {max_score:>2}")       # ➋
# endless loop until a valid option is choosen
while True:                                                 # ➌
    command = input("Type the number for an option: >>>")
    try:                                                 
        number = int(command)                               # ➍
    except ValueError:
        print("not a number, please try again")
        continue                                            # ➎ 
    if not (1 <= number <= 13):                             # ➏
        print("not a valid number, please try again")
        continue
    option = list(all_options.keys())[number-1]             # ➐
    break
print("you choose to play", option )

output

output of dicegame01_04c.txt

diff

diff between dicegame01_04b.py -> dicegame01_04c.py

--- /home/horst/code/sphinx_playground/source/dicegame/dicegame01_04b.py
+++ /home/horst/code/sphinx_playground/source/dicegame/dicegame01_04c.py
@@ -1,4 +1,4 @@
-# dictionary of option name and maximum score
+# dictionary: key: option name, value:  maximum score
 all_options = {  
                                        # upper section:
            "Ones":            5,
@@ -17,19 +17,22 @@
            "Chance":          30,
            }
 
-# string with l3 letters for menu options
-abc = "abcdefghijklm"
-
 # write menu and display maximum points for each option
 print("please choose one option of those:")
 print("letter  name         max. score")
-for letter, (name, max_score) in zip(abc,all_options.items()): # ➊
-    print(f"{letter:>5}: {name:<15}  {max_score:>2}")          # ➋
+for number, (name, max_score) in enumerate(all_options.items(), 1): # ➊
+    print(f"{number:>2}: {name:<15}  {max_score:>2}")       # ➋
 # endless loop until a valid option is choosen
-while True:                                                    # ➌
-    command = input("Type the letter for an option: >>>")
-    if len(command) == 1 and command in abc:                   # ➍
-        option = list(all_options.keys())[abc.index(command)]  # ➎
-        break
-    print("strange input. Please try again.")
+while True:                                                 # ➌
+    command = input("Type the number for an option: >>>")
+    try:                                                 
+        number = int(command)                               # ➍
+    except ValueError:
+        print("not a number, please try again")
+        continue                                            # ➎ 
+    if not (1 <= number <= 13):                             # ➏
+        print("not a valid number, please try again")
+        continue
+    option = list(all_options.keys())[number-1]             # ➐
+    break
 print("you choose to play", option )

code explained

➀:

A lot happens in this line, let’s break it down:

1. enumerate() gives an index to all the items of the dictionary all_options. This index would normally start with 0, but here a second argument is given to the enumerate function so that the index starts with 1.

2. The for loop iterates over the result of enumerate and assigns values to the variables number, name and max_score.

➁:

printing a beautiful menu using f-string. The numbers behind the colon inside of the curly brackets align the strings and give them a minimum width. See Format Specification Mini Language.

➂:

Create an endless loop because nobody can predict how many attempts the user needs before they will make a valid choice. The indented code block below (lines 27-37) will be repeated as often as necessary.

➃:

This conversion of a string into an integer is done isnside of a try block. If Python can not convert into an integer (for example, because the user generated an empty string py pressing Enter without typing something) an ValueError is raised, but the program jumps to line 30 instead of stooping.

➄:

continue forces the program flow back to the beginning of the current loop… back to line 27.

➅:

the same as:

if (number < 1) or (number > 13):

➆:

the keys of the dictionary all_options are converted into a list. From this list, the element with the index (number-1) is assigned to the variable option

The code below uses a dictionary to store the option_names and the maximum_score, and uses another dictionary named history to store the name of the played_option (as key) and as value a tuple: the achived score for this option and a copy of dicelist.

Because the functions to calculate the score for each option are not written yet, this version gives for each played option the maximum possible score:

dicgame01_05.py

source code

import random
history = {}            # ➊ 
dicelist = []    
all_options = {         # ➋
                                       # upper section:
           "Ones":            5,
           "Twos":            10,
           "Threes":          15,
           "Fours":           20,
           "Fives":           25,
           "Sixes":           30,
                                        # lower section
           "Three Of A Kind": 30,
           "Four Of A Kind":  30,
           "Full House":      25,
           "Small Straight":  30,
           "Large Straight":  40,
           "Yahtzee":         50,
           "Chance":          30,
           }
for game_round in range(1,14):                    
    dicelist = []                                     
    for _ in range(5):    
        dicelist.append(random.randint(1,6))  
    print(f"-------- round {game_round} of 13--------------")  
    for throw in (1,2,3):                         
        text= "throw: {} of 3".format(throw)      
        print(text)
        print(" a  b  c  d  e")
        print(dicelist)
        if throw < 3:
            text = "Type letter(s) of dice to keep and press ENTER >>>"
            command = input(text).lower()              
            for i, char in enumerate("abcde") :         
                if char not in command:                
                    dicelist[i] = random.randint(1,6)   

    print(f"------- end of round {game_round}------")
    # calculate playable options    # ➌
    unplayed = [name for name in all_options if name not in history]
    while True:                     # ➍ 
        # create menu, starting with number 1 for "Ones"
        for name in unplayed:     
            print(list(all_options).index(name)+1, name) # ➎ 
        command = input("enter number of option to play >>>")
        try:                         # ➏
            number = int(command)    # ➐
        except ValueError:           # ➑
            print("Please enter only a NUMBER")
            continue                 # ➒
        if not (0 < number < 14):    # ➓
            print("Number out of allowed range, try again")
            continue                 # ➒
        #try:
        option = list(all_options)[number-1] # ⓫ 
        #except IndexError:
        #    print("Please enter only a listed number")
        #    continue
        if option not in unplayed:   # ⓬ 
            print(f"You already played {option}, try again")
            continue                 # ➒
        print("You play: ", option)
        break                        # ⓭
    # option should be correct now
    points = all_options[option]     # ⓮ 
    print(f"you get {points} points!")
    if game_round == 13:                       
        text = "press ENTER to see the history of dice throws >>>"
    else:
        text = "press ENTER to start the next game round >>>"
    input(text)                            
    history[option] = (points, dicelist.copy())  # ⓯
print("Game Over")  
print("--- history of your dice throws: ---")
print("game round,  played_option, points, dicelist")
for game_round, played  in enumerate(history, 1):   
    score, result = history[played]   # ⓰
    print("{:>5}: {}  {:<20}  points: {:>3} ".format(
          game_round, result, played, score )) # ⓱
          

output

example output of dicegame01_05.txt (Your output may be different)

-------- round 1 of 13--------------
throw: 1 of 3
 a  b  c  d  e
[5, 4, 1, 5, 2]
Type letter(s) of dice to keep and press ENTER >>>ad
throw: 2 of 3
 a  b  c  d  e
[5, 5, 1, 5, 6]
Type letter(s) of dice to keep and press ENTER >>>abd
throw: 3 of 3
 a  b  c  d  e
[5, 5, 3, 5, 5]
------- end of round 1------
1 Ones
2 Twos
3 Threes
4 Fours
5 Fives
6 Sixes
7 Three Of A Kind
8 Four Of A Kind
9 Full House
10 Small Straight
11 Large Straight
12 Yahtzee
13 Chance
enter number of option to play >>>5
You play:  Fives
you get 25 points!
press ENTER to start the next game round >>>

--snip--

You play:  Full House
you get 25 points!
press ENTER to see the history of dice throws >>>
Game Over
--- history of your dice throws: ---
game round,  played_option, points, dicelist
    1: [5, 5, 3, 5, 5]  Fives                 points:  25 
    2: [1, 3, 1, 4, 3]  Ones                  points:   5 
    3: [1, 3, 3, 3, 3]  Threes                points:  15 
    4: [4, 2, 1, 6, 4]  Twos                  points:  10 
    5: [4, 4, 4, 1, 6]  Fours                 points:  20 
    6: [5, 3, 1, 5, 2]  Sixes                 points:  30 
    7: [2, 1, 6, 6, 4]  Three Of A Kind       points:  30 
    8: [4, 4, 4, 4, 4]  Yahtzee               points:  50 
    9: [5, 6, 5, 4, 3]  Small Straight        points:  30 
   10: [3, 6, 3, 3, 3]  Four Of A Kind        points:  30 
   11: [2, 1, 2, 6, 3]  Chance                points:  30 
   12: [3, 4, 1, 2, 6]  Large Straight        points:  40 
   13: [6, 2, 6, 3, 6]  Full House            points:  25 

diff

diff between dicegame01_04.py -> dicegame01_05.py

--- /home/horst/code/sphinx_playground/source/dicegame/dicegame01_04.py
+++ /home/horst/code/sphinx_playground/source/dicegame/dicegame01_05.py
@@ -1,34 +1,81 @@
 import random
-
-history = []                                      
-   
-for game_round in range(1,14):                    # ➊ 
+history = {}            # ➊ 
+dicelist = []    
+all_options = {         # ➋
+                                       # upper section:
+           "Ones":            5,
+           "Twos":            10,
+           "Threes":          15,
+           "Fours":           20,
+           "Fives":           25,
+           "Sixes":           30,
+                                        # lower section
+           "Three Of A Kind": 30,
+           "Four Of A Kind":  30,
+           "Full House":      25,
+           "Small Straight":  30,
+           "Large Straight":  40,
+           "Yahtzee":         50,
+           "Chance":          30,
+           }
+for game_round in range(1,14):                    
     dicelist = []                                     
     for _ in range(5):    
         dicelist.append(random.randint(1,6))  
-    print(f"-------- round {game_round} of 13--------------")  # ➋
-    for throw in (1,2,3):                         # ➌
-        text= "throw: {} of 3".format(throw)      # ➍
+    print(f"-------- round {game_round} of 13--------------")  
+    for throw in (1,2,3):                         
+        text= "throw: {} of 3".format(throw)      
         print(text)
         print(" a  b  c  d  e")
         print(dicelist)
         if throw < 3:
-            text = "Type letter(s) of dice to keep and press ENTER "
-            command = input(text).lower()              # ➎
-            for i, char in enumerate("abcde") :        # ➏ 
+            text = "Type letter(s) of dice to keep and press ENTER >>>"
+            command = input(text).lower()              
+            for i, char in enumerate("abcde") :         
                 if char not in command:                
-                    dicelist[i] = random.randint(1,6)  # ➐ 
+                    dicelist[i] = random.randint(1,6)   
 
-        
     print(f"------- end of round {game_round}------")
-    if game_round == 13:                       # ➑
-        text = "press ENTER to see the history of dice throws"
+    # calculate playable options    # ➌
+    unplayed = [name for name in all_options if name not in history]
+    while True:                     # ➍ 
+        # create menu, starting with number 1 for "Ones"
+        for name in unplayed:     
+            print(list(all_options).index(name)+1, name) # ➎ 
+        command = input("enter number of option to play >>>")
+        try:                         # ➏
+            number = int(command)    # ➐
+        except ValueError:           # ➑
+            print("Please enter only a NUMBER")
+            continue                 # ➒
+        if not (0 < number < 14):    # ➓
+            print("Number out of allowed range, try again")
+            continue                 # ➒
+        #try:
+        option = list(all_options)[number-1] # ⓫ 
+        #except IndexError:
+        #    print("Please enter only a listed number")
+        #    continue
+        if option not in unplayed:   # ⓬ 
+            print(f"You already played {option}, try again")
+            continue                 # ➒
+        print("You play: ", option)
+        break                        # ⓭
+    # option should be correct now
+    points = all_options[option]     # ⓮ 
+    print(f"you get {points} points!")
+    if game_round == 13:                       
+        text = "press ENTER to see the history of dice throws >>>"
     else:
-        text = "press ENTER to start the next game round"
-    input(text)                           # ➒  
-    history.append(dicelist.copy())       # ➓
+        text = "press ENTER to start the next game round >>>"
+    input(text)                            
+    history[option] = (points, dicelist.copy())  # ⓯
 print("Game Over")  
 print("--- history of your dice throws: ---")
-print("game round,  result")
-for game_round, result in enumerate(history, 1):  # ⓫ 
-    print(f"{game_round:>5} : {result}" )         # ⓬+print("game round,  played_option, points, dicelist")
+for game_round, played  in enumerate(history, 1):   
+    score, result = history[played]   # ⓰
+    print("{:>5}: {}  {:<20}  points: {:>3} ".format(
+          game_round, result, played, score )) # ⓱
+          
+

code explained

➀:

history is now a dictionary, with the name of the played option as key and the tuple (score, dicelist) as value

➁:

all_options is a dictionary with the option name as key and the maximum possible score as value

➂:

At the end of each game round (after the third throw), the list unplayed is calculated by an list comprehension.

➃:

The player must enter a valid choice here, and it is not forseeable how many attempts they will need. Therefore the construction using an endless loop until a the user types in an acceptable choice.

➄:

What this code line does:

1. transforms the keys of the dictionary all_options into a list

2. finds out the index of name in this list. (name is the name of an unplayed option, like “Full House”)

3. adds 1 to this index, so that the option “Ones” has the value 1 instead of 0

4. print the number (index+1) and name, separated by a space

➅:

the indented line below (line 48) is inside a try-block and will not stop the program when an exception is raised (when something goes wrong): Instead, the code block below except will be executed. (line 50+51).

➆:

Try to convert the string command into an integer and assign it to the variable number.

➇:

If the try-block above (line 48) throws a ValueError exception, the except-block below (line 50+51) is executed. A ValueError occurs for example when a string can not be converted into an integer using int().

➈:

The continue command puts the program flow back to the beginning of the while loop (line 42)

➉:

if the value of number (it’s an integer now) is not between 1 and 13

⑪:

Calculating the selected option from the entered menu number. What happens here step by step:

1. the keys of the dictionary all_options are converted into a list

2. the correct index position is calculated (because the menu starts with 1 but Python starts indexing a list with 0). Therefore, number - 1 is the correct index for Python.

3. the value of the element number - 1 of this list is assigned to the variable option. (The value is a string, like “Full House”)

⑫:

Checks if the value of the variable option (A string like “Full House”) is not inside the list unplayed.

⑬:

The break command breaks out of the while loop, the program flow continues in line 65

⑭:

option is a string like “Full House”. This code line makes a lookup operation: It looks into the dictionary all_options, searches for a key (the value of the variable option) and returns the the value of this dictioary… the maximum possible score for this option (an integer). This number is assigned to the variable points.

⑮:

creates a new entry into the dictionary history: the key is the name of the played option, the value is a tuple: (points and a copy of dicelist).

⑯:

the value of the dictionary history is a tuple with two values: (points and a copy of dicelist). Both values are assigned to the two variables score and result. This line could also be written in two seperate lines:

score = history[played][0]
result = history[played][1]

⑰:

The chars inside of the curly brackets are formating commands (see Format Specification Mini Language):

• {:>5} right aligns the variable game_round and gives it a minimum length of 5 chars.

• {:<20} left aligns the variable played and gives it a minimum length of 20 chars

• {:>3} right aligns the variable score and gives it a minimum length of 3 chars

The game is (somewhat) playable now! Only the score calculation does not work yet correctly, because the player gets the maximum possible score for each option, no matter what they throw.

• simulate throwing 5 dice

• let the player keep some dice / throw some dice

• keep track of game round and throws

• ask the player to choose an option and keep track of played options

• show the player which options they can play

• show the player how many points they will get for each option

• calculate sum of points at the end of the game

step four

task:

show the player how many points they will get for each option

task:

calculate sum of points at the end of the game

This is by far the most complex step. To calculate how many points an playable option is worth, two steps are necessary:

1. To check if the conditions for the option are met by the numbers inside the variable dicelist.

2. To calculate how many points the option would bring according to the rules of the game, because not all options give a fixed amount of points.

While not strictly necessary, it is a good idea to create a few functions to test if dicelist meets the conditions for each option. Those functions will return either True (if the conditions are met) or False.

It is good practice to prefix names of functions that return an boolean value with is_: A function to test if dicelist is a “Full House” should be named: is_full_house(). Such an function name indicates already that the function will return either True or False. (Another way to indicate what the function returns is using a type hint and/or a docstring).

By tradition (and more specific, by the rules of the Python style guide PEP8), function names should always be written in lowercase. A space in a function name is not allowed but underscores are allowed.

Note

All the functions described below require at least one parameter named dice. This is technically not necessary: If dicelist is defined in the global scope (at “root level”), then the function can access dicelist and does not need to have it passed as a parameter.

Those two examples below both work correctly:

function without parameter

# function without parameters
def is_yahtzee():
    if len(set(dicelist)) == 1:
        return True
    return False
    
# dicelist is defined at root level
dicelist = [1,4,4,4,2]
# call function:
result = is_yahtzee()
print(result)

function with parameter

# function with parameter
def is_yahtzee(dice):
    if len(set(dice)) == 1:
        return True
    return False
    
#  root level
dicelist = [1,4,4,4,2]
# call function with one argument
result = is_yahtzee(dicelist)
print(result)

The functions below will all use the variant with a parameter named dice. To work correctly, each function call has to pass dicelist as argument to the function.

is_three_of_a_kind()

This function takes a look at dicelist (actually, at the parameter dice) and returns True if dice is a “Three of a kind”, otherwise the function returns False. As always, there exist more than one single way of how to code such a function. The variant below uses the list.count() functionality of lists.

Included in the code example below is some (very simple) code for testing if the function works correctly. See doctest and unittest to take a deeper look into testing with Python.

dicgame01_06.py

source code

def is_three_of_a_kind(dice):              # ➊
    """dice is a list of five integers"""  # ➋ 
    for number in dice:                    # ➌
        if dice.count(number) >= 3:        # ➍
            return True                    # ➎
    return False                           # ➏

if __name__ == "__main__":
    # tests   
    print("testing...")
    assert is_three_of_a_kind([1,1,2,2,2]) == True # ➐
    assert is_three_of_a_kind([1,1,2,2,2]) == True
    assert is_three_of_a_kind([1,1,2,2,2]) == True
    assert is_three_of_a_kind([1,4,4,4,4]) == True
    assert is_three_of_a_kind([5,5,5,5,5]) == True
    assert is_three_of_a_kind([1,2,3,4,5]) == False
    assert is_three_of_a_kind([2,3,4,5,6]) == False
    assert is_three_of_a_kind([1,1,2,2,5]) == False
    assert is_three_of_a_kind([6,1,4,6,1]) == False
    assert is_three_of_a_kind([6,1,1,1,2]) == True
    print("all tests passed")    # ➑

output

output of dicegame01_06.txt

testing...
all tests passed

code explained

➀:

the function definition: starting with the keyword def, the function name is_three_of_a_kind and one parameter named dice. The lines 2-6 are the function body.

➁:

A docstring in triple quotes.

➂:

iterating over all elements of dice. Each element is assigned to the variable number.

➃:

If one element inside dice occours three times or more often…

➄:

… then the function returns True because dice qualifies as a “Three Of A Kind”.

➅:

If the for loop runs through the function returns False.

➆:

Testing the function: by using assert, Python looks if the expression right of assert is True. If yes, then the testing was sucessfull. If not, the program stops with an Assertation Error message. The expression right of assert is a function call using a list (a dicelist) as argument. The return value of this function call is compared with an boolean value.

➇:

The line will only be executed if all lines before passed without Error.

Attention

What would happen if you add an test that does not work? For example, add this line, run the program and check the output:

assert is_three_of_a_kind([1,1,1,2,2]==False)

is_four_of_a_kind()

The list.count() functionality of lists can also be used to detect “Four Of A Kind”.

dicgame01_06.py

source code

def is_four_of_a_kind(dice):               # ➊
    """dice is a list of five integers"""  # ➋ 
    for number in dice:                    # ➌
        if dice.count(number) >= 4:        # ➍
            return True                    # ➎
    return False                           # ➏

if __name__ == "__main__":
    # tests   
    print("testing...")
    assert is_four_of_a_kind([1,2,3,4,5]) == False # ➐
    assert is_four_of_a_kind([1,1,2,2,2]) == False
    assert is_four_of_a_kind([2,1,2,2,2]) == True
    assert is_four_of_a_kind([4,4,4,4,4]) == True
    print("all tests passed")    # ➑

output

output of dicegame01_07.txt

testing...
all tests passed

code explained

➀:

the function definition: starting with the keyword def, the function name is_four_of_a_kind and one parameter named dice. The lines 2-6 are the function body.

➁:

A docstring in triple quotes.

➂:

iterating over all elements of dice. Each element is assigned to the variable number.

➃:

If one element inside dice occours four times or more often…

➄:

… then the function returns True because dice qualifies as a “Four Of A Kind”.

➅:

If the for loop runs through the function returns False.

➆:

Testing the function: by using assert, Python looks if the expression right of assert is True. If yes, then the testing was sucessfull. If not, the program stops with an Assertation Error message. The expression right of assert is a function call using a list (a dicelist) as argument. The return value of this function call is compared with an boolean value.

➇:

The line will only be executed if all lines before passed without Error.

is_full_house()

A “Full House” is defined as dicelist having 2 equal numbers and 3 (other) equal numbers. In other words, only 2 different numbers exist inside dicelist, one of them occuring three times, the other one occuring 2 times.

As always, there exist several ways of how to code a function to detect if dicelist is a “Full House”. The code example below creates a set out of dicelist (to be more exact, out of the parameter dice) and assign this set to the variable diceset. By definition, there can be only unique values (no duplicate values) in a set. If diceset has a length of 2 and those numbers exist 2 or 3 times in dice, the function returns True. Otherwise, the function returns False.

dicgame01_08.py

source code

def is_full_house(dice):                      # ➊
    """dice is a list of five integers"""     # ➋ 
    diceset = set(dice)                       # ➌
    if len(diceset) == 2:                     # ➍
        for number in diceset:                # ➎
            if dice.count(number) in (2,3):   # ➏
                return True                   # ➐
    return False                              # ➑

if __name__ == "__main__":
    # tests   
    print("testing...")
    assert is_full_house([1,2,3,4,5]) == False    # ➒ 
    assert is_full_house([1,1,2,2,2]) == True
    assert is_full_house([6,4,6,4,6]) == True
    assert is_full_house([4,4,4,4,4]) == False
    print("all tests passed")                     # ➓

output

output of dicegame01_08.txt

testing...
all tests passed

code explained

➀:

the function definition: starting with the keyword def, the function name is_full_house and one parameter named dice. The lines 2-8 are the function body.

➁:

A docstring in triple quotes.

➂:

creating a set out of the list dice and storing it into the variable diceset

➃:

If diceset consist of exactly 2 elements….

➄:

… then iterate over each element in diceset

➅:

If this element occurs 2 or 3 times in dice then….

➆:

return True.

➇:

If the for loop runs through, return False.

➈:

Testing the function: by using assert, Python looks if the expression right of assert is True. If yes, then the testing was sucessfull. If not, the program stops with an Assertation Error message. The expression right of assert is a function call using a list (a dicelist) as argument. The return value of this function call is compared with an boolean value.

➉:

The line will only be executed if all lines before passed without Error.

is_small_straight()

A “Small Straight” is defines as dicelist having those numbers: [1,2,3,4] or [2,3,4,5] or [3,4,5,6]. The numbers can be in any order, of course.

Sets offer functionality to test if one set is a superset or a subset of another set. In other words, it is very easy to test if all numbers inside of a small set also exist in a bigger set.

dicgame01_09.py

source code

def is_small_straight(dice):                  # ➊
    """dice is a list of five integers"""     # ➋ 
    diceset = set(dice)                       # ➌
    if any((diceset.issuperset({1,2,3,4}),    # ➍
            diceset.issuperset({2,3,4,5}),
            diceset.issuperset({3,4,5,6}))):
        return True                           # ➎
    return False                              # ➏

if __name__ == "__main__":
    # tests   
    print("testing...")
    assert is_small_straight([1,2,3,4,1]) == True    # ➐ 
    assert is_small_straight([6,5,4,3,2]) == True
    assert is_small_straight([2,3,4,5,2]) == True
    assert is_small_straight([3,4,5,6,6]) == True
    assert is_small_straight([4,4,4,4,4]) == False
    assert is_small_straight([1,2,2,3,6]) == False
    print("all tests passed")                     # ➑

output

output of dicegame01_09.txt

testing...
all tests passed

code explained

➀:

the function definition: starting with the keyword def, the function name is_small_straight and one parameter named dice. The lines 2-7 are the function body.

➁:

A docstring in triple quotes.

➂:

creating a set out of the list dice and storing it into the variable diceset

➃:

This line could also be written as:

if ((diceset >= {1,2,3,4}) or
    (diceset >= {2,3,4,5}) or
    (diceset >= {3,4,5,6})):
    return True

It means: If any() of those three conditions are True:

• diceset is a superset of {1,2,3,4} or

• diceset is a superset of {2,3,4,5} or

• diceset is a superset of {3,4,5,6} then…

➄:

… return True

➅:

otherwise, return False

➆:

Testing the function: by using assert, Python looks if the expression right of assert is True. If yes, then the testing was sucessfull. If not, the program stops with an Assertation Error message. The expression right of assert is a function call using a list (a dicelist) as argument. The return value of this function call is compared with an boolean value.

➉:

The line will only be executed if all lines before passed without Error.

is_large_straight()

A “Large Straight” must contain the numbers [1,2,3,4,5] or [2,3,4,5,6] (in any order). The code is very similar to the code above:

dicgame01_10.py

source code

def is_large_straight(dice):                  # ➊
    """dice is a list of five integers"""     # ➋ 
    diceset = set(dice)                       # ➌
    if (diceset.issuperset({1,2,3,4,5}) or    # ➍
        diceset.issuperset({2,3,4,5,6})):
        return True                           # ➎
    return False                              # ➏

if __name__ == "__main__":
    # tests   
    print("testing...")
    assert is_large_straight([1,2,3,4,5]) == True    # ➐ 
    assert is_large_straight([6,5,4,3,2]) == True
    assert is_large_straight([2,3,4,5,2]) == False
    assert is_large_straight([3,4,5,6,6]) == False
    assert is_large_straight([4,4,4,4,4]) == False
    assert is_large_straight([1,3,4,5,6]) == False
    print("all tests passed")                     # ➑

output

output of dicegame01_10.txt

testing...
all tests passed

code explained

➀:

the function definition: starting with the keyword def, the function name is_large_straight and one parameter named dice. The lines 2-7 are the function body.

➁:

A docstring in triple quotes.

➂:

creating a set out of the list dice and storing it into the variable diceset

➃:

This line could also be written as:

if ((diceset >= {1,2,3,4,5}) or
    (diceset >= {2,3,4,5,6})):
    return True

It means that if diceset is a superset of {1,2,3,4,5} or of {2,3,4,5,6} then…

➄:

… return True

➅:

otherwise, return False

➆:

Testing the function: by using assert, Python looks if the expression right of assert is True. If yes, then the testing was sucessfull. If not, the program stops with an Assertation Error message. The expression right of assert is a function call using a list (a dicelist) as argument. The return value of this function call is compared with an boolean value.

➉:

The line will only be executed if all lines before passed without Error.

is_yahtzee()

How to test if a dicelist is a “Yathzee”: The most simple variant is to compare all numbers using the == operator:

def is_yahtzee(dice):
    """dice is a list of five integers"""
    return dice[0] == dice[1] == dice[2] == dice[3] == dice[4]
    

Another variant is by using a set: If all numbers inside a dicelist are the same, the set of this dicelist has a length of exactly one:

dicgame01_11.py

source code

def is_yahtzee(dice):                      # ➊
    """dice is a list of five integers"""  # ➋ 
    return len(set(dice)) == 1             # ➌
    
if __name__ == "__main__":
    # tests   
    print("testing...")
    assert is_yahtzee([1,2,3,4,5]) == False    # ➍ 
    assert is_yahtzee([6,5,6,6,6]) == False
    assert is_yahtzee([2,2,2,2,2]) == True
    assert is_yahtzee([2,4,4,2,2]) == False
    print("all tests passed")                  # ➎

output

output of dicegame01_11.txt

testing...
all tests passed

code explained

➀:

the function definition: starting with the keyword def, the function name is_yahtzee and one parameter named dice. The lines 2-3 are the function body.

➁:

A docstring in triple quotes.

➂:

This single code line does all the work: Starting to read with the innermost brackets, the code does:

1. create a set out of the list dice (it is not assigned to a variable but simply used)creating a set out of the list dice and

2. calculate the length of this set by using the len() function (it counts how many elements are in this set).

3. compare this value (how many elements are in the set) with the number 1. If the resulting expression is a boolean value. Either it is 1 == 1 (equals True) or it is something else, like 4 == 1 and equals False. The 9boolean value value is the return value of the function.

➃:

Testing the function: by using assert, Python looks if the expression right of assert is True. If yes, then the testing was sucessfull. If not, the program stops with an Assertation Error message. The expression right of assert is a function call using a list (a dicelist) as argument. The return value of this function call is compared with an boolean value.

➄:

The line will only be executed if all lines before passed without Error.

calculate_score()

Now what is missing is a function to calculate the score for a given dicelist and a given option.

The first six keys of the dictionary all_options are the “upper section”: (“Ones”, “Twos”, “Threes” etc.). All of those six options are very easy to calculate: The desired number (1 for “Ones” etc.) is multiplyed by the frequency (how many times 1 occurs inside dicelist).

For example, if dicelist contains two time the number 6 and the player choose to play “Sixes”, the calculation is 2 x 6 = 12 points.

The score for the options “Three of a kind”, “Four of a kind” and “Chance” is also very easy to calculate: just take the sum of all dice in dice. Python provides a sum() functions for lists, so the code is simply score = sum(dice).

The scores for “Full House”, “Small Straight”, “Large Straight” and “Yahtzee” are fixed with 25, 30, 40 and 50 points.

Finally, there is the joker rule: If a “Yahtzee” was already played AND another Yahtzee is thrown AND this (new) “Yahtzee” can not be played in the corresponding field of the upper section anymore THEN this Yahtzee acts as a joker for “Full House” / “Small Straight” / “Large Straight”, giving 25 / 30 / 40 points.

The code snippet below calls all the little functions listed above (is_full_house(), is_three_of_a_kind()) and therefore needs to either include those functions or import them:

dicgame01_12.py

source code

# this program can NOT run by itself!  # ➊➋➌

def calculate_score(dice, name_of_option): # ➍
    """calculate how much points an option would score using dice""" # ➎   
    # assert expression, error_message
    assert len(dice) == 5, f"{dice} must have five elements" # ➏
    error_message = f"{dice} must have only integers"
    assert [type(x) for x in dice] == [int,int,int,int,int], error_message # ➐
    error_message = f"{name_of_option} must be in {all_options.keys()}"
    assert name_of_option in all_options, error_message # ➑

    # joker rule?
    option_list = list(all_options) # ➒
    joker = False
    upper_name = option_list[dice[0]-1] # ➓
    if all((is_yahtzee(dice),           # ⓫
            "Yahtzee" in history,
            upper_name in history)):
        joker = True
    match name_of_option:               # ⓬
        # first test the lower section options
        case "Three Of A Kind":
            return sum(dice) if is_three_of_a_kind(dice) else 0 # ⓭
        case "Four Of A Kind":
            return sum(dice) if is_four_of_a_kind(dice) else 0
        case  "Full House":
            return 25 if (is_full_house(dice) or joker) else 0
        case  "Small Straight":
            return 30 if (is_small_straight(dice) or joker) else 0
        case "Large Straight":
            return 40 if (is_large_straight(dice) or joker) else 0
        case "Yahtzee":
            return 50 if is_yahtzee(dice) else 0
        case "Chance":
            return sum(dice)
        case _:  # ⓮
            # it's an upper section option:  Ones, Tows, ... Sixes
            number = option_list.index(name_of_option) + 1 # ⓯
            return dice.count(number) * number             # ⓰

code explained

➀➁➂:

dicegame01_12.py can not run in any meaningful way by itself, it needs functions and data structures from other programs. Among others it needs:

• the dictionary all_options

• the dictionary history

• several functions to test for “lower section” options, like is_three_of_a_kind etc. Of course you can start dicegame01_12.py but nothing will happen: The program includes only a single function (calculate_score() but no function call.

➃:

Defining the function calculate_score(). This line is the function definition. This function has two parameters: dice (a list of five dice numbers) and name_of_option, a string from the all_options dictionary.

➄:

This line is a docstring in triple quotes. The docstring describes the function.

➅:

The first of several guardians to see if the function got correct arguments. This line checks if dice consist of five elements. The assert statement makes sure an expression is True. If the expression is not True, the python program stops by raising an AssertionError and writing an error message. This line could also be written with an if statement:

if len(dice) != 5:
    raise AssertionError, f"{dice} must have five elements"

➆:

This guardian uses another assert statement to thest if dice consist only of integers. This is done by creating a list comprehension first: [type(x) for x in dice]. The result should be a list with the types of the elements of dice: [int, int, int, int, int]. If there would be for some strange reason non-integer elements inside dice (like float or string) the program would stop with an AssertionError and display the error_message.

➇:

The last guardian of this function makes sure that name_of_option is an existing key of the all_options dictionary.

➈:

The same as option_list = list(all_options.keys()) … it creates a real list out of the keys of the dictionary all_options.

➉:

This is a bit difficult: What happens here is that a value is assigned to the variable upper name. What value? The name of the option to play in the “upper section” of the playable options, corresponding to the first numer in the list dice. Let’s describe it step by step:

1. Get the first element of dice: dice[0] (it is an integer)

2. Substract 1 from this first element. Example: The first element was a 6, the result after the subtraction is 5.

3. Use this calculated number (5 in the example) as an index for option_list. Like every list in python, the index starts with 0. The element with the index 5 is “Sixes”.

4. Assign this string (“Sixes”) to the variable upper_name.

⑪:

Test if the joker rule (see Game rules) can be used: Three conditions must be fullfilled:

• dice is a “Yahtzee”

• “Yahtzee” was already played

• The corresponding “upper section” is already played. This line of code uses the all() function to test if all of those three conditions are True. The code could also be written using and operators:

if (is_yahtzee(dice) and 
    ("Yahtzee" in history) and
    (upper_name in history)):
    joker = True

⑫:

Instead of writing a big block of if, elif, else statements the match syntax is used here: the value of the variable name_of_option is matched:

⑬:

inline if: This code is equivalent to this code block:

if is_three_of_a_kind(dice):
    return sum(dice)
else:
    return 0

⑭:

The underscore _ catches all other cases, like an else statement. Because all previous cases were “lower section” options and because the guardian at ➇ made sure that name_of_option is a key of all_options, the value of name_of_option must now be an “upper section” option. For all of those, the score calculation is done by the same formula.

⑮:

Calculating the integer value if the upper section name is given. Step by step:

1. find out the index of name_of_option inside of option_list. Example: name_of_option is “Fives”. This is the fifth element of option_list but python starts indexing with 0! The index is therefore 4.

2. Add 1 to the result. (Example: 4+1 = 5). Assign this integer vlaue to the variable number.

⑯:

Look how often number exist in the list dice using the list.count() method. (Example: dice is [5,5,2,3,2] and number is 5. Five exist inside dice two times. The return value is therefore 5 * 2 = 10)

Note that the code example below has no output. To see what the function calculate_score() returns, it is necessary to write another program, a specific test program.

testing calculate_score()

This is done here in dicegame01_13.py. It includes the function calculate_score() but without comments (for comments explaining the function, see dicegame01_12.py above). It also includes the functions is_three_of_a_kind() etc. from the programs dicegame01_06.py etc. (see far above) by making use of python’s import command. Finally, the dictionaries history and all_options are included (and manipulated!) to test a lot of different dice combinations (using python’s assert command).

dicgame01_13.py

source code

from dicegame01_06 import is_three_of_a_kind # ➊
from dicegame01_07 import is_four_of_a_kind
from dicegame01_08 import is_full_house
from dicegame01_09 import is_small_straight
from dicegame01_10 import is_large_straight
from dicegame01_11 import is_yahtzee

def calculate_score(dice, name_of_option): # ➋
    """calculate how much points an option would score using dice"""    
    # assert expression, error_message
    assert len(dice) == 5, f"{dice} must have five elements" 
    error_message = f"{dice} must have only integers"
    assert [type(x) for x in dice] == [int,int,int,int,int], error_message 
    error_message = f"{name_of_option} must be in {all_options.keys()}"
    assert name_of_option in all_options, error_message 

    # joker rule?
    option_list = list(all_options) # 
    joker = False
    upper_name = option_list[dice[0]-1] # 
    if all((is_yahtzee(dice),           # 
            "Yahtzee" in history,
            upper_name in history)):
        joker = True
    match name_of_option:               # 
        # first test the lower section options
        case "Three Of A Kind":
            return sum(dice) if is_three_of_a_kind(dice) else 0 # ⓭
        case "Four Of A Kind":
            return sum(dice) if is_four_of_a_kind(dice) else 0
        case  "Full House":
            return 25 if (is_full_house(dice) or joker) else 0
        case  "Small Straight":
            return 30 if (is_small_straight(dice) or joker) else 0
        case "Large Straight":
            return 40 if (is_large_straight(dice) or joker) else 0
        case "Yahtzee":
            return 50 if is_yahtzee(dice) else 0
        case "Chance":
            return sum(dice)
        case _:  
            # it's an upper section option:  Ones, Tows, ... Sixes
            number = option_list.index(name_of_option) + 1 # ⓯
            return dice.count(number) * number             # ⓰


history = {}            # ➌ 
all_options = {         # ➍
                                       # upper section:
           "Ones":            5,
           "Twos":            10,
           "Threes":          15,
           "Fours":           20,
           "Fives":           25,
           "Sixes":           30,
                                        # lower section
           "Three Of A Kind": 30,
           "Four Of A Kind":  30,
           "Full House":      25,
           "Small Straight":  30,
           "Large Straight":  40,
           "Yahtzee":         50,
           "Chance":          30,
           }


print("testing...")  # ➎
assert calculate_score([1,1,1,1,3], "Ones") == 4 
assert calculate_score([1,2,2,2,3], "Twos") == 6
assert calculate_score([1,1,1,2,3], "Threes") == 3
assert calculate_score([1,1,1,2,3], "Fours") == 0
assert calculate_score([1,1,5,2,3], "Fives") == 5
assert calculate_score([6,6,6,6,6], "Sixes") == 30
assert calculate_score([1,1,1,2,3], "Three Of A Kind") == 8
assert calculate_score([1,1,2,2,3], "Three Of A Kind") == 0
assert calculate_score([1,1,1,1,1], "Three Of A Kind") == 5
assert calculate_score([2,2,2,2,3], "Four Of A Kind") == 11
assert calculate_score([2,2,2,3,3], "Four Of A Kind") == 0
assert calculate_score([2,2,2,2,2], "Four Of A Kind") == 10
assert calculate_score([2,2,2,3,3], "Full House") == 25
assert calculate_score([2,2,2,2,3], "Full House") == 0
assert calculate_score([2,2,2,2,2], "Full House") == 0
assert calculate_score([1,2,3,4,5], "Small Straight") == 30
assert calculate_score([2,3,4,5,6], "Small Straight") == 30
assert calculate_score([1,3,4,5,6], "Small Straight") == 30
assert calculate_score([5,4,3,2,2], "Small Straight") == 30
assert calculate_score([5,5,6,3,4], "Small Straight") == 30
assert calculate_score([1,3,3,4,6], "Small Straight") == 0
assert calculate_score([2,2,3,3,3], "Small Straight") == 0
assert calculate_score([2,2,2,2,2], "Small Straight") == 0
assert calculate_score([1,2,3,4,5], "Large Straight") == 40
assert calculate_score([2,3,4,5,6], "Large Straight") == 40
assert calculate_score([5,6,3,4,2], "Large Straight") == 40
assert calculate_score([1,2,3,4,1], "Large Straight") == 0
assert calculate_score([1,2,3,6,5], "Large Straight") == 0
assert calculate_score([1,1,1,1,1], "Large Straight") == 0
assert calculate_score([1,2,3,1,5], "Chance") == 12
assert calculate_score([1,1,1,1,1], "Yahtzee") == 50
assert calculate_score([1,1,1,1,2], "Yahtzee") == 0
# joker rule: put "Ones" and "Yahtzee" in history
history = {"Ones":None,  # the values are not important now
        "Yahtzee":None,
        }
#print(history) # ➏
assert calculate_score([1,1,1,1,1], "Small Straight") == 30 # ➍
assert calculate_score([1,1,1,1,1], "Large Straight") == 40
assert calculate_score([1,1,1,1,1], "Full House") == 25
print("all tests passed")

output

output of dicegame01_13.txt

testing...
all tests passed

code explained

➀:

In lines 1-6 several functions are imported from other python programs. Note that only the file extension (.py) is not written in the import commands, only the module name (the filename witout the file extension, like dicegame01_06 instead of dicegame01_06.py).

➁:

The function calculate_score() is defined here (with a bit extra work, it could be imported from dicegame01_12.py instead). To see the comments explaining what the function does, please see the code example dicegame01_12.py above.

➂:

defining an empty dictionary with the name history. It will later be manipulated to test the joker rule.

➃:

defining the dictionary all_options. The keys of this dictionary are the option names, the values of this dictionary are the maximum possible points for each option.

➄:

Testing if a specific list of dice and a specific played option gives indeed the expected score.

➅:

Testing the joker rule: history is filled with entries for “Ones” and “Yahtzee” already. According to the joker rule, an additional Yahtzee can then act as “Small Straight”, “Large Straight” or “Full House”

Nearly all sub-tasks are now done:

• simulate throwing 5 dice

• let the player keep some dice / throw some dice

• keep track of game round and throws

• ask the player to choose an option and keep track of played options

• show the player how many points they will get for each option

• calculate sum of points at the end of the game

step five

last remaining task:

calculate the sum of points at the end of the game

Two specific rules need to be checked before calculating the final score of a Yahtzee game:

upper section bonus:

If the sum of the upper section options (“Ones”, “Twos”,…”Sixes”) is equal or larger than 63. If yes, an “Upper section bonus” of 35 points is added to the final score.

Yahtzee bonus:

Not to be confused with the Joker rule (where Yahtzee can act as a joker for Full House etc): The Yahtzee bonus rule checks if Yahtzee was already played sucessfully with 50 points. If yes and if another Yahtzee is rolled, a bonus of 100 points is added to the final score. This bonus applies to each (additional) Yahtzee in a game. For example, if a super lucky player manages to roll a Yathzee in the first game round (played as “Yahtzee” with 50 points) and in the same game manages to roll two additional Yathzees, they would score an Yathzee bonus of 200 points.

Here is a function to calculate the sum of the upper section options, the upper section bonus, the sum of the lower section options and the yahtzee bonus. The final score is the sum of those 4 values. The program below includes the function and a few tests:

dicgame01_14.py

source code

def calculate_final_scores(history):   # ➊
    """returns a tuple of 4 integers: 
           sum_upper_section,
           upper_section_bonus,
           sum_lower_section,
           yahtzee_bonus
    """                                # ➋
    sum_upper_section = 0              # ➌
    sum_lower_section = 0
    upper_section_bonus = 0
    yahtzee_bonus = 0
    allow_yahtzee_bonus = False
    for name in history:               # ➍     
        scored = history[name][0]      # ➎
        dice = history[name][1]        # ➏
        # is upper section?            # ➐
        if name in ("Ones", "Twos", "Threes",
                    "Fours", "Fives", "Sixes"):
            sum_upper_section += scored
        else:
            sum_lower_section += scored
        # is Yahtzee?                  # ➑
        if len(set(dice)) == 1: 
            # enable Yahtzee bonus ?
            if scored == 50 and not allow_yahtzee_bonus:
                allow_yahtzee_bonus = True
            elif allow_yahtzee_bonus:
                yahtzee_bonus += 100
    if sum_upper_section >= 63:        # ➒
        upper_section_bonus = 35
    return sum_upper_section, upper_section_bonus, sum_lower_section, yahtzee_bonus

# testing

if __name__ == "__main__":             # ➓       
    print("testing...")
    # example 1:
    # get upper section bonus of 35
    # because sum(upper_section) > 63
    history = {"Ones":  (5, [1,1,1,1,1]),
               "Twos":  (10,[2,2,2,2,2]),
               "Threes":(15,[3,3,3,3,3]),
               "Fours": (20,[4,4,4,4,4]),
               "Fives": (15,[5,5,5,1,1]),
               "Sixes": (0,[1,2,6,6,3]),
               }
    assert sum(calculate_final_scores(history)) == 100
    # test the upper section bonus  directly
    # it's the second element of the return value 
    # a second element in python has the index 1
    assert calculate_final_scores(history)[1] == 35
    # example 2:
    # get yahtzee bonus of 100:
    history = {"Ones":   (5, [1,1,1,1,1]),
               "Yahtzee":(50, [2,2,2,2,2]),
               "Twos":   (10, [2,2,2,2,2])}        
    assert sum(calculate_final_scores(history)) == 165        
    # example 3
    # get yahtzee bonus of 200:
    history = {"Ones":   (5, [1,1,1,1,1]),
               "Yahtzee":(50, [2,2,2,2,2]),
               "Twos":   (10, [2,2,2,2,2]),
               "Threes": (15, [3,3,3,3,3])}        
    assert sum(calculate_final_scores(history)) == 280        
    # example4: 
    # don't get yahtzee bonus because Yahtzee
    # because Yahtzee was played (used up) with
    # zero points already:
    history = {"Ones":(5, [1,1,1,1,1]),
               "Yahtzee":(0, [3,4,2,2,2]),
               "Twos":(10, [2,2,2,2,2])}        
    assert sum(calculate_final_scores(history)) == 15        
    
    print("all tests passed")

output

output of dicegame01_14.txt

testing...
all tests passed

code explained

➀:

The function definition accept only one parameter named history: a dictionary of option names as keys and a tuple of score and dicelist as values.

➁:

The docstring inside triple quotes explains what the function is doing. The docstring here spans over several lines

➂:

A bunch of variables are declared in lines 8-12. As the calculation of the final scores has not started yet, the value of zero (in one case: False) is assigned all those variables.

➃:

iterating over the keys of the dictionary history

➄:

the values of the dictionary history are tuples: (score, dicelist). The first element of the tuple has the index 0 (the score), the second element has the index 1. The score is assigned to the variable scored.

➅:

the second element of the tuple is assigned to the variable dice.

➆:

Line 17-21: Checks if the played option (name) is a “upper section” option. If yes, then the value of scored is added to sum_upper_sectoin. Otherwise, the value of scored is added to sum_lower_section.

➇:

Testing for the Yahtzee bonus: Line 23 is a copy of the is_Yahtzee() function: The set of Yahtzee has always the length of 1. If the list dice is indeed a Yahtzee, line 25 checks if it scored 50 points in history (played as Yahtzee) and only in this case sets allow_yahtzee_bonus to True if it was not True already. The elif command in line 27 checks if allow_yahtzee_bonus is True and if yes adds 100 to yahtzee_bonus.

➈:

Checks if the value of sum_upper_section is greater or equal of 63. If yes, the upper_section_bonus is set to 35.

➉:

If the program dicegame01_14.py is started directly (and not imported from another program) it runs the tests (lines 36-70). All those tests create a history dictionary and then test if the function calculate_final_score produce the desired outcome. Note that only a few tests are provided here.

This was the final sub-task!

• simulate throwing 5 dice

• let the player keep some dice / throw some dice

• keep track of game round and throws

• ask the player to choose an option and keep track of played options

• show the player how many points they will get for each option

• calculate sum of points at the end of the game

merging everything together

The end of this tutorial is reached. The last task is to merge all the “little” functions together into one big python program that can run alone. Note that tests and detailed comments can be found in the code examples above.

dicgame01_15.py

source code

import random
history = {}            # ➊ 
all_options = {         # ➋
                                       # upper section:
           "Ones":            5,
           "Twos":            10,
           "Threes":          15,
           "Fours":           20,
           "Fives":           25,
           "Sixes":           30,
                                        # lower section
           "Three Of A Kind": 30,
           "Four Of A Kind":  30,
           "Full House":      25,
           "Small Straight":  30,
           "Large Straight":  40,
           "Yahtzee":         50,
           "Chance":          30,
           }

# functions to test options

def is_three_of_a_kind(dice):              # 
    """dice is a list of five integers"""  #  
    for number in dice:                    # 
        if dice.count(number) >= 3:        # 
            return True                    # 
    return False  

def is_four_of_a_kind(dice):               # 
    """dice is a list of five integers"""  #  
    for number in dice:                    # 
        if dice.count(number) >= 4:        # 
            return True                    # 
    return False  

def is_full_house(dice):                      # 
    """dice is a list of five integers"""     #  
    diceset = set(dice)                       # 
    if len(diceset) == 2:                     # 
        for number in diceset:                # 
            if dice.count(number) in (2,3):   # 
                return True                   # 
    return False                              # 

def is_small_straight(dice):                  # 
    """dice is a list of five integers"""     #  
    diceset = set(dice)                       # 
    if any((diceset.issuperset({1,2,3,4}),    # 
            diceset.issuperset({2,3,4,5}),
            diceset.issuperset({3,4,5,6}))):
        return True                           # 
    return False                          

def is_large_straight(dice):                  # 
    """dice is a list of five integers"""     #  
    diceset = set(dice)                       # 
    if (diceset.issuperset({1,2,3,4,5}) or    # 
        diceset.issuperset({2,3,4,5,6})):
        return True                           # 
    return False   

def is_yahtzee(dice):                      # 
    """dice is a list of five integers"""  #  
    return len(set(dice)) == 1             # 
    
def calculate_score(dice, name_of_option): # 
    """calculate how much points an option would score using dice"""    
    # assert expression, error_message
    assert len(dice) == 5, f"{dice} must have five elements" 
    error_message = f"{dice} must have only integers"
    assert [type(x) for x in dice] == [int,int,int,int,int], error_message 
    error_message = f"{name_of_option} must be in {all_options.keys()}"
    assert name_of_option in all_options, error_message 

    # joker rule?
    option_list = list(all_options) # 
    joker = False
    upper_name = option_list[dice[0]-1] # 
    if all((is_yahtzee(dice),           # 
            "Yahtzee" in history,
            upper_name in history)):
        joker = True
    match name_of_option:               # 
        # first test the lower section options
        case "Three Of A Kind":
            return sum(dice) if is_three_of_a_kind(dice) else 0 # 
        case "Four Of A Kind":
            return sum(dice) if is_four_of_a_kind(dice) else 0
        case  "Full House":
            return 25 if (is_full_house(dice) or joker) else 0
        case  "Small Straight":
            return 30 if (is_small_straight(dice) or joker) else 0
        case "Large Straight":
            return 40 if (is_large_straight(dice) or joker) else 0
        case "Yahtzee":
            return 50 if is_yahtzee(dice) else 0
        case "Chance":
            return sum(dice)
        case _:  
            # it's an upper section option:  Ones, Tows, ... Sixes
            number = option_list.index(name_of_option) + 1 # 
            return dice.count(number) * number             # 

def calculate_final_scores(history):   # 
    """returns a tuple of 4 integers: 
           sum_upper_section,
           upper_section_bonus,
           sum_lower_section,
           yahtzee_bonus
    """                                # 
    sum_upper_section = 0              # 
    sum_lower_section = 0
    upper_section_bonus = 0
    yahtzee_bonus = 0
    allow_yahtzee_bonus = False
    for name in history:               #      
        scored = history[name][0]      # 
        dice = history[name][1]        # 
        # is upper section?            # 
        if name in ("Ones", "Twos", "Threes",
                    "Fours", "Fives", "Sixes"):
            sum_upper_section += scored
        else:
            sum_lower_section += scored
        # is Yahtzee?                  # 
        if len(set(dice)) == 1: 
            # enable Yahtzee bonus ?
            if scored == 50 and not allow_yahtzee_bonus:
                allow_yahtzee_bonus = True
            elif allow_yahtzee_bonus:
                yahtzee_bonus += 100
    if sum_upper_section >= 63:        # 
        upper_section_bonus = 35
    return sum_upper_section, upper_section_bonus, sum_lower_section, yahtzee_bonus

# main function

def game():
    for game_round in range(1,14):                    
        dicelist = []                                     
        for _ in range(5):    
            dicelist.append(random.randint(1,6))  
        print(f"-------- round {game_round} of 13--------------")  
        for throw in (1,2,3):                         
            text= "throw: {} of 3".format(throw)      
            print(text)
            print(" a  b  c  d  e")
            print(dicelist)
            if throw < 3:
                text = "Type letter(s) of dice to keep and press ENTER >>>"
                command = input(text).lower()              
                for i, char in enumerate("abcde") :         
                    if char not in command:                
                        dicelist[i] = random.randint(1,6)   

        print(f"------- end of round {game_round}------")
        # calculate playable options    # 
        unplayed = [name for name in all_options if name not in history]
        while True:                     #  
            # create menu, starting with number 1 for "Ones"
            for name in unplayed:     
                print(list(all_options).index(name)+1, name) #  
            command = input("enter number of option to play >>>")
            try:                         # 
                number = int(command)    # 
            except ValueError:           # 
                print("Please enter only a NUMBER")
                continue                 # 
            if not (0 < number < 14):    # 
                print("Number out of allowed range, try again")
                continue                 # 
            #try:
            option = list(all_options)[number-1] #  
            #except IndexError:
            #    print("Please enter only a listed number")
            #    continue
            if option not in unplayed:   # 
                print(f"You already played {option}, try again")
                continue                 # 
            print("You play: ", option)
            break                        # 
        # option should be correct now
        #points = all_options[option]     #  
        points = calculate_score(dicelist, option)
        print(f"you get {points} points!")
        if game_round == 13:                       
            text = "press ENTER to see the history of dice throws >>>"
        else:
            text = "press ENTER to start the next game round >>>"
        input(text)                            
        history[option] = (points, dicelist.copy())  # 
    print("Game Over")  
    print("--- history of your dice throws: ---")
    print("game round,  played_option, points, dicelist")
    sum_upper, upper_bonus, sum_lower, yat_bonus = calculate_final_scores(history)
    print("option,          score (of max.)    dice")
    for name in all_options:
        print("{:<20}   {:>2} (of {:>2})   {:<20}".format(
            name,
            history[name][0],
            all_options[name],
            str(history[name][1])
        ))
        if name == "Sixes":
            print("-------------------------")
            print("sum upper section:", sum_upper)
            print("upper section bonus:", upper_bonus)
    print("--------------------")
    print("sum lower section", sum_lower)
    print("Yahtzee bonus:", yat_bonus)
    print("==========================")
    print("final score:",
           sum_upper+upper_bonus+sum_lower+yat_bonus)
    
            


if __name__ == "__main__":
    game()

output

output of dicegame01_15.txt

---(snip)----
Game Over
--- history of your dice throws: ---
game round,  played_option, points, dicelist
option,          score (of max.)    dice
Ones                    1 (of  5)   [6, 4, 1, 4, 4]     
Twos                    0 (of 10)   [5, 1, 3, 6, 4]     
Threes                  0 (of 15)   [4, 5, 4, 4, 2]     
Fours                   0 (of 20)   [6, 6, 5, 1, 2]     
Fives                   0 (of 25)   [2, 3, 4, 1, 2]     
Sixes                   0 (of 30)   [1, 4, 1, 1, 3]     
-------------------------
sum upper section: 1
upper section bonus: 0
Three Of A Kind        21 (of 30)   [1, 5, 5, 5, 5]     
Four Of A Kind          8 (of 30)   [1, 1, 1, 4, 1]     
Full House              0 (of 25)   [6, 6, 3, 4, 4]     
Small Straight          0 (of 30)   [6, 3, 3, 2, 3]     
Large Straight          0 (of 40)   [4, 2, 3, 2, 3]     
Yahtzee                 0 (of 50)   [6, 4, 3, 5, 1]     
Chance                 16 (of 30)   [4, 5, 5, 1, 1]     
--------------------
sum lower section 45
Yahtzee bonus: 0
==========================
final score: 46

code explained

➀:

create empty dictionary history. The keys of this dictionary are the names of the played options, the values of this dictionary are tuples: (score, dicelist)

➁:

create dictionary all_options. The keys of this dictionary are the name of the options, the values are the maximal possible scores for each option.